【Create my OS】3 内存管理

November 22, 2024

Github代码仓库链接

本章将对操作系统可使用的内存进行管理，有两种管理粒度：按页分配和任意粒度分配。

按页分配有助于我们实现下一章的页表
任意粒度分配则属于动态内存分配，类似于 C 语言的 malloc 函数。
本章将先实现按任意粒度（64Bytes）的动态内存分配
再实现按页分配的页帧分配

3.1 Buddy System

Buddy System Allocation 是一种经典的内存分配算法，同时也是Linux 内核底层所使用的内存分配算法，动态内存分配也打算使用此算法来管理堆内存。

1、伙伴分配的实质就是一种特殊的“分离适配”，即将内存按2的幂进行划分，相当于分离出若干个块大小一致的空闲链表，搜索该链表并给出同需求最佳匹配的大小。

优点是快速搜索合并（O(logN) 时间复杂度）以及低外部碎片（最佳适配）；
缺点是内部碎片，因为按2的幂划分块，如果碰上分配 66 个单位，那么必须划分 128 单位的块。

2、算法描述

分配内存

寻找大小合适的内存块（大于等于所需大小并且最接近2的幂）
1. 如果找到了，就返回这个块
2. 否则，分出合适的内存块
  1. 对半分开大于所需大小的空闲内存块
  2. 如果分到最低限度，就返回这个块
  3. 返回到步骤 1（继续寻找合适大小的块）

释放内存

释放该内存块
1. 寻找相邻的内存块，查看其是否已被释放
2. 如果被释放了，就合并这两个块，重复上述操作直到遇到未被释放的相邻块，或者达到上限。

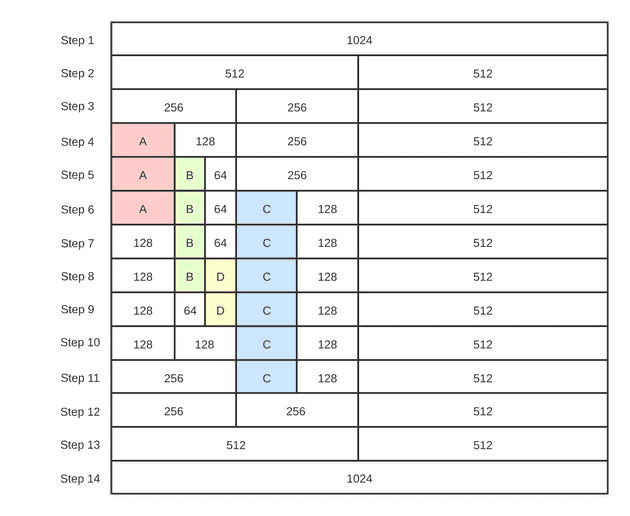
3、算法图解，只需要看一下图解10个步骤，对应例子和上述的算法描述，就能够理解这个算法了。这个例子中，我们要进行一下步骤：

分配一个 100 单位大小的块 A
分配一个 60 单位大小的块 B
分配一个 100 单位大小的块 C
释放块 A
分配一个 30 单位大小的块 D
释放块 B
释放块 D
释放块 C

总内存空间 1024 个单位大小，最小分配单位为 64 单位。图示如下：

4、算法实现

我们使用一棵二叉树来存储每一级范围内的最大连续空闲块个数，譬如上面的例子，二叉树的第一层就存储了整块 1024 单位的范围内的最大连续空闲块个数，第二层两个节点就分别存储了两个 512 单位块范围内的最大连续空闲块个数。二叉树的最下层就代表了每个具体的块是否被使用了，也就是 0 和 1。当然，这些个数都是 2 的幂级数。

// kernle/heap.c

/* 
 * Buddy System Allocation 的具体实现
 * 使用一棵数组形式的完全二叉数来监控内存
 */
struct
{
    int size;                    /* 管理的总块数 */
    int longest[BUDDY_NODE_NUM]; /* 每个节点表示范围内最大连续空闲块个数 */
    // 二叉树总节点个数 BUDDY_NODE_NUM = size*2 - 1
} buddyTree;

初始化二叉树

// 二叉树初始化
void
buddyInit(int size)
{
    buddyTree.size = size;      // 管理的总块数
    int nodeSize = size << 1;   // 因为下为对于i=0节点也会判断为2的幂，所以先乘2来抵消下文的除2
    int i;
    /* 初始化每个节点，此时每一块都是空闲的 */
    for(i = 0; i < (size << 1) - 1; i ++) {
        // 若当前节点为2的幂，则除以2
        if(IS_POWER_OF_2(i+1)) {
            nodeSize /= 2;
        }
        buddyTree.longest[i] = nodeSize;    
        // 数组存储例：1024 512 512 256 256 256 256 128 128...
    }
}

分配块：选择满足条件的最小的分叉。如果左右子树都满足条件（必然有一个会满足），就会选择值最小的那个子树。

/* 
 * 试图分配 size 大小的块，返回空闲块的第一块在堆上的偏移
 * 该版本的分配过程是从上往下搜索，寻找大小最合适的节点
 */
int
buddyAlloc(int size)
{
    int index = 0;
    int nodeSize;
    int offset;

    /* 调整内存块数量到 2 的幂 */
    if(size <= 0) size = 1;
    else if(!IS_POWER_OF_2(size)) size = fixSize(size);

    /* 超过总内存分配大小 */
    if(buddyTree.longest[0] < size) {
        return -1;
    }
    
    /* 从二叉树根开始，寻找大小最符合的节点 */
    for(nodeSize = buddyTree.size; nodeSize != size; nodeSize /= 2) {   // 不断减小nodeSize，直到和size一样大
        int left = buddyTree.longest[LEFT_LEAF(index)];     // 左子节点索引结果，即大小
        int right = buddyTree.longest[RIGHT_LEAF(index)];   // 右子结点索引结果，即大小
        /* 优先选择最小的且满足条件的分叉，小块优先，尽量保留大块 */
        if(left <= right) {
            if(left >= size) index = LEFT_LEAF(index);  // 大小满足，继续向下找
            else index = RIGHT_LEAF(index);
        } else {
            if(right >= size) index = RIGHT_LEAF(index);
            else index = LEFT_LEAF(index);
        }
    }

    /* 
     * 将该节点标记为占用
     * 注意这里标记将该节点的下级节点，便于回收时确定内存块数量
     */
    buddyTree.longest[index] = 0;

    /* 获得这一段空闲块的第一块在堆上的偏移 */
    offset = (index + 1) * nodeSize - buddyTree.size;

    /* 向上调整父节点的值,即空闲个数 */
    while(index) {
        index = PARENT(index);
        buddyTree.longest[index] = 
            MAX(buddyTree.longest[LEFT_LEAF(index)], buddyTree.longest[RIGHT_LEAF(index)]);
    }

    return offset;
}

回收块：注意我们在分配块的时候，只将该块标记为占用，而没有将其子块标记。譬如，我们分配一个 128 单位的块，仅仅是表示该块的节点被标记，但是其子块：两个 64 单位的块的节点仍然被标记为未占用。这种做法不会影响块的分配，因为寻找空闲块是自顶向下，从根节点开始寻找的。同时，它还有利于根据块号回收区间。从最小块向上回溯，一直回溯到第一个被标记为全部占用的节点，就是我们当时分配出去的节点。
回收的过程很简单，将这个节点改为未占用，并继续向上回溯，修改上级节点的占用情况。

/* 根据 offset 回收区间 */
void
buddyFree(int offset)
{
    int nodeSize, index = 0;
    
    nodeSize = 1;
    index = offset + buddyTree.size - 1;

    /* 
     * 向上回溯到之前分配块的节点位置
     * 由于分配时没有标记下级节点，这里只需要向上寻找到第一个被标记的节点就是当时分配的节点
     */
    for( ; buddyTree.longest[index]; index = PARENT(index)) {  // 直到被标记为0则退出
        nodeSize *= 2;
        if(index == 0) {    // 到根节点还没有被占用，直接退出
            return;
        }
    }
    buddyTree.longest[index] = nodeSize;    // 恢复空闲大小

    /* 继续向上回溯，合并连续的空闲区间，直到根节点 */
    while(index) {
        index = PARENT(index);
        nodeSize *= 2;

        int leftLongest, rightLongest;
        leftLongest = buddyTree.longest[LEFT_LEAF(index)];
        rightLongest = buddyTree.longest[RIGHT_LEAF(index)];

        // 如果左、右根节点的空闲大小之和等于父节点空闲大下
        if(leftLongest + rightLongest == nodeSize) {
            buddyTree.longest[index] = nodeSize;    // 则合并（修改父节点最大连续大小）
        } else {
            buddyTree.longest[index] = MAX(leftLongest, rightLongest);  // 否则父节点取子结点最大连续大小
        }
    }
}

注意：此处除了上述新建的kernel/heap.c文件，还建立了kernel/consts.h头文件来存放一些系统常量，如下所示：

// kernel/consts.h

#ifndef CONSTS_H
#define CONSTS_H

/* 动态内存中定义堆的相关常量 */
#define BUDDY_NODE_NUM      0x3ffff             /* 二叉树节点个数 */

#endif

3.2 动态内存分配

1、实现 kalloc

我们可以直接声明一个 8M 大数组，作为堆空间，用于动态内存分配，还定义一些构造 Buddy System 所使用的常量。

// kernel/consts.h
/* 动态内存中定义堆的相关常量 */
#define KERNEL_HEAP_SIZE    0x800000            /* 堆空间大小 */
#define MIN_BLOCK_SIZE      0x40                /* 最小分配的内存块大小 */
#define HEAP_BLOCK_NUM      0x20000             /* 管理的总块数 */
#define BUDDY_NODE_NUM      0x3ffff             /* 二叉树节点个数 HEAP_BLOCK_NUM*2-1 */

// kernel/heap.c
static uint8 HEAP[KERNEL_HEAP_SIZE];

按照 C 语言的接口，实现两个函数。分别是 usize *kalloc(uint32 size) 和 void kfree(void *ptr)。其实内部主要就是调用上一节实现的 buddyAlloc() 和 buddyFree() 函数，只是对输入数据进行了一些处理而已。
kalloc() 函数首先获取所需分配的内存块数，之后就调用 buddyAlloc()，返回的分配的内存空间的第一个内存块号。
我们可以将其转换成相对于堆空间起始地址的偏移，进一步得到实际的地址。但是在返回之前，我们首先需要清空这一块内存，将其内容全写为 0。

// kernle/heap.c

/*
 * 获得大于等于某个数的最小的 2 的幂级数
 * 算法来源于 Java HashMap 实现
 */
int
fixSize(int size)
{
    int n = size - 1;
    n |= n >> 1;
    n |= n >> 2;
    n |= n >> 4;
    n |= n >> 8;
    n |= n >> 16;
    return n + 1;
}

/* 
 * 在堆上分配内存
 * 输入：size，单位为 Byte
 * 输出：分配空间的起始地址
*/
void *
kalloc(int size)
{
    if(size <= 0) return 0;

    uint32 n;
    // 计算需要分配的块数
    if((size && (MIN_BLOCK_SIZE-1)))    // 分配块数 与 最小分配块数-1 相与不为零，说明右余数，块数+1
        n = size / MIN_BLOCK_SIZE + 1;
    else
        n = size / MIN_BLOCK_SIZE;
    // 分配块，得到偏移地址（单位为MIN_BLOCK_SIZE）
    int block = buddyAlloc(n);
    if(block == -1) panic("Malloc failed!\n");

    /* 清零被分配的内存空间 */
    int totalBytes = fixSize(n) * MIN_BLOCK_SIZE;   // 计算所分配的大小，单位bytes
    // 计算分配空间的起始地址(usize)，声明指向一个字节(uint8)的指针指向这个地址
    uint8 *beginAddr = (uint8 *)((usize)HEAP + (usize)(block * MIN_BLOCK_SIZE));
    int i;
    for(i = 0; i < totalBytes; i ++) {  // 逐字节清零分配的内存空间
        beginAddr[i] = 0;
    }
    
    return (void *)beginAddr;   
}

2、实现 kfree()

回收的过程就很简单了，我们将传入的地址转换成相对于堆起始地址的偏移，进而转换成块号，最后调用 buddyFree() 即可

/* 
 * 回收被分配出去的内存 
 * 输入：回收空间的起始地址
*/
void
kfree(void *ptr)
{
    // 验证地址是否在堆空间
    if((usize)ptr < (usize)HEAP) return;
    if((usize)ptr > (usize)HEAP + KERNEL_HEAP_SIZE - MIN_BLOCK_SIZE) return;
    /* 相对于堆空间起始地址的偏移 */
    usize offset = (usize)((usize)ptr - (usize)HEAP);
    buddyFree(offset / MIN_BLOCK_SIZE);
}

3、测试内存分配

我们定义一个 initHeap() 函数，并且在其中调用 buddyInit()
来编写一个测试函数，我们的最小分配单位和上一届中的那个例子一致，都是 64

// kernel/heap.c

// 初始化堆空间
void
initHeap()
{
    buddyInit(HEAP_BLOCK_NUM);
}

void
testHeap()
{
    printf("Heap:\t%p\n", HEAP);
    void *a = kalloc(100);
    printf("a:\t%p\n", a);
    void *b = kalloc(60);
    printf("b:\t%p\n", b);
    void *c = kalloc(100);
    printf("c:\t%p\n", c);
    kfree(a);
    void *d = kalloc(30);
    printf("d:\t%p\n", d);
    kfree(b);
    kfree(d);
    kfree(c);
    a = kalloc(60);
    printf("a:\t%p\n", a);
    kfree(a);
}

在main()函数中调用

void main()
{
    extern void initInterrupt();    initInterrupt();    // 设置中断处理程序入口 和 模式
    extern void initTimer();        initTimer();        // 时钟中断初始化

    // asm volatile("ebreak" :::); // 手动触发一个中断
    // printf("return from ebreak\n");
    extern void initHeap();         initHeap(); 
    extern void testHeap();         testHeap();

    while(1) {}
}

可以得到如下输出结果（与上图示分配结果一致）：

==== Init Interrupt ====
Heap:    0x0000000080311000
a:    0x0000000080311000
b:    0x0000000080311080
c:    0x0000000080311100
d:    0x00000000803110c0
a:    0x0000000080311000

4、管理内存开销分析

采用 Buddy System Allocation 算法需要维护 BuddyTree，我们可以来分析一下其占用的内存空间。对于本节所使用的8M堆空间（2^23）
若设置最小分配的块大小为 16 Byte = 2^4 Byte，则总共有 2^19 个块，管理的满二叉树有 2^20 - 1 个结点，每个结点都是四字节大小的无符号整数，则占用空间 2^22 Byte = 4M，我们管理一个 8M 的空间就需要多花费 4M 的内存！这有点得不偿失。
若最小分配的块大小为 64Byte = 2^6 byte。则只需要 2^20 Byte = 1M，勉强算在可接受范围内了。

3.3 内存按页分配框架

1、物理地址是用于访问物理内存的，物理内存可以看作一个很大的字节数组，而物理地址就是它的下标。但事实上，物理地址不仅仅能访问物理内存，很多指令集架构提供了一种技术 MMIO（Memory Mapped I/O），可以将外部设备映射到物理地址空间，这样我们访问外设时就可以像访问物理内存一样简单了。

在 OpenSBI 初始化时，会自动探测所有的外设（包括物理内存）的地址，并将结果保存在设备树（DTB，Device Tree Blob）中，供操作系统使用。 QEMU 模拟的 RISC-V Virt 的物理地址空间布局可以在 QEMU 的代码中查找到：

static const struct MemmapEntry {
    hwaddr base;
    hwaddr size;
} virt_memmap[] = {
    [VIRT_DEBUG] =       {        0x0,         0x100 },
    [VIRT_MROM] =        {     0x1000,        0xf000 },
    [VIRT_TEST] =        {   0x100000,        0x1000 },
    [VIRT_RTC] =         {   0x101000,        0x1000 },
    [VIRT_CLINT] =       {  0x2000000,       0x10000 },
    [VIRT_PCIE_PIO] =    {  0x3000000,       0x10000 },
    [VIRT_PLIC] =        {  0xc000000, VIRT_PLIC_SIZE(VIRT_CPUS_MAX * 2) },
    [VIRT_UART0] =       { 0x10000000,         0x100 },
    [VIRT_VIRTIO] =      { 0x10001000,        0x1000 },
    [VIRT_FLASH] =       { 0x20000000,     0x4000000 },
    [VIRT_PCIE_ECAM] =   { 0x30000000,    0x10000000 },
    [VIRT_PCIE_MMIO] =   { 0x40000000,    0x40000000 },
    [VIRT_DRAM] =        { 0x80000000,           0x0 },
};

我们可以不用关心前面的内容，只关心数组的最后一个元素，VIRT_DRAM。这个元素描述的就是我们可以使用的 DRAM 物理内存，起始地址为 0x80000000，长度被定义为 0x0，实际上，这段内存的长度可以在启动 QEMU 时通过 -m 参数指定，默认是 128M。所以我们可以使用的物理内存地址范围为（ 0x80000000, 0x88000000 )。

2、操作系统分配内存，多数情况下是以一个页，即连续的 4K 字节为单位分配的。每一个页都可以被一个物理页号（Physical Page Number，PPN）来唯一表示，通常一个物理页的页号是这个页的起始地址除以 4K，或者说，右移 12 位。一个物理页所表示的范围就是 [ PPN << 12, (PPN + 1) << 12 )（一个 Page table entire,PTE 由 PPN + Flags 组成）

在 kernel/memory.h 中定义一些常量

// kernel/memory.h

extern void kernel_end();                       /* 内核所在内存空间结束的虚拟地址 */

#define PAGE_SIZE           4096                /* 页/帧大小 */
#define MEMORY_START_PADDR  0x80000000          /* 可以访问的内存区域起始地址 */
#define MEMORY_END_PADDR    0x88000000          /* 可以访问的内存区域结束地址 */
#define KERNEL_BEGIN_PADDR  0x80200000          /* 内核起始的物理地址 */
#define KERNEL_BEGIN_VADDR  0x80200000          /* 内核起始的虚拟地址 */

kernel_end 是我们在kernel.ld链接脚本中定义的一个符号，表示内核的结束地址，这里我们可以以外部函数的方式引用过来。目前，内核起始和结束的物理地址和虚拟地址相同。
我们定义一个 FrameAllocator 结构，用于真正进行物理页的分配和回收。
其中 Allocator 结构体代表一种具体的分配/回收算法，定义如下。

// kernel/memory.h

/* 具体的页帧分配/回收算法实现结构体 */
typedef struct
{
    usize (*alloc)(void);           // 分配页帧的函数指针
    void (*dealloc)(usize index);   // 回收页帧的函数指针
} Allocator;

/* 页帧分配/回收管理器 */
typedef struct
{
    usize startPpn;         /* 可用空间的起始 */
    Allocator allocator;    /* 具体的分配/回收实现算法 */
} FrameAllocator;

3、内存按页分配框架

接着我们定义一个全局的 FrameAllocator，并且实现一些全局的接口，如 allocFrame() 和 deallocFrame()，当然这些函数还是调用的具体实现算法 Allocator 的函数，仅仅是一层包装而已。allocFrame() 函数还顺便把分配的物理页给清空了。

/* 全局唯一的页帧分配器 */
FrameAllocator frameAllocator;

/* 分配算法需要实现的三个函数 */
Allocator newAllocator(usize startPpn, usize endPpn);
usize alloc();                                           
void dealloc(usize ppn);

// 初始化全局页帧分配器
void
initFrameAllocator(usize startPpn, usize endPpn)
{
    frameAllocator.startPpn = startPpn;     // 设置分配器的起始页帧号
    frameAllocator.allocator = newAllocator(startPpn, endPpn);  // 初始化页帧分配器
}

/*
 * 分配一个物理页
 * 返回物理页的起始地址
 */
usize
allocFrame()
{
    // 分配一个物理页并计算地址
    char *start = (char *)(alloc() << 12);
    int i;
    // 初始化页的每个字节为零
    for(i = 0; i < PAGE_SIZE; i ++) {
        start[i] = 0;
    }
    return (usize)start;
}

/*
 * 回收一个物理页
 * 输入为物理页的起始物理地址
 */
void
deallocFrame(usize startAddr)
{
    dealloc(startAddr >> 12);
}

下一节，我们来实现一个基于线段树的页帧分配算法，并真正地进行物理页分配。

3.4 基于线段树的页帧分配

1、本节将实现具体的页帧分配算法，其实就是实现三个函数：

// kernel/memory.c

// 分配算法的三个关键函数
Allocator newAllocator(usize startPpn, usize endPpn);
usize alloc();
void dealloc(usize ppn);

2、将采用一棵非递归线段树来实现，和3.1节提到的 Buddy System Allocation 算法的结构非常类似，同样也是一棵二叉树管理 2 的幂级数长度的区间，只不过，我们并不要记录该区间上还有多少空闲页，因为我们一次只分配一页。这样，每个节点只需要记录一个 boolean（布尔值），即该区间上是否有空闲页。

假设需要有 MAX_PHYSICAL_PAGSE 个物理页，实际上肯定不会用掉这么多空间，因为内核也占据了一部分可用内存的一部分，实际可分配的页会小于该值。

/* 最大可用的内存长度，从 0x80000000 ~ 0x88000000 */
#define MAX_PHYSICAL_PAGES 0x8000   // 页大小为4K

// 管理页栈分配的线段树结构
struct
{
    uint8 node[MAX_PHYSICAL_PAGES << 1];    /* 线段树的节点，每个都表示该范围内是否有空闲页 */
    usize firstSingle;                      /* 第一个单块节点的下标，即最后一层叶子节点的下标 */
    usize length;                           /* 分配区间长度，表示可分配的页帧数量 */
    usize startPpn;                         /* 分配的起始 ppn */
} sta;

3、初始化线段树

初始化的过程很简单，传入的参数是要分配区间的起始 PPN 和结束 PPN，主要内容就是填充 node 数组。

// kernel/memory.c

// 初始化页帧分配器（线段数初始化）
Allocator
newAllocator(usize startPpn, usize endPpn)
{
    sta.startPpn = startPpn - 1;
    sta.length = endPpn - startPpn;     // 设置页帧分配的区间长度
    sta.firstSingle = 1;

    // 找到合适的树大小，树的节点数量必须是2的幂
    while(sta.firstSingle < sta.length + 2) {   // 推测：+1是因为尾-头，头和尾本身也是节点；又+1是因为firstSingle要大于区间长度
        sta.firstSingle <<= 1;
    }

    // 初始化线段树每个节点为1，表示已分配了
    usize i = 1;
    for(i = 1; i < (sta.firstSingle << 1); i ++) {  // 完全二叉树总节点个数为管理节点数乘2
        sta.node[i] = 1;
    }
    // 初始化叶子节点为0（线段树末端），表示页帧是空闲的
    for(i = 1; i < sta.length; i ++) {
        sta.node[sta.firstSingle + i] = 0;
    }
    // 构建线段树，将左右子节点的值与运算，如果左右子节点有一个是空闲的，那父节点也是空闲块
    for(i = sta.firstSingle - 1; i >= 1; i --) {
        sta.node[i] = sta.node[i << 1] & sta.node[(i << 1) | 1];
    }
    Allocator ac = {alloc, dealloc};    // 创建分配器
    return ac;
}

最后创建了一个 Allocator，传入了两个参数，分别是 alloc 函数和 dealloc 函数，就是我们下面要实现的。

4、分配页面

之前我们在3.2节动态内存分配那一节，专门要求要 best-fit 而不是 first-fit，以防止出现过多的外部碎片。然而这里，只是用 first-fit 就可以了，因为我们分配的单位固定是一个页，而如果内存区间有空余，那最小也是一个页大小。

// kernel/memory.c

/*
 * 分配一个物理页
 * 返回物理页号 PPN 
 */
usize
alloc()
{
    // 如果根节点已分配，表示没有空闲页
    if(sta.node[1] == 1) {
        panic("Physical memory depleted!\n");
    }
    // 查找空闲页
    usize p = 1;
    while(p < sta.firstSingle) {    // p 小于单节点地址
        if(sta.node[p << 1] == 0) { // 判断左子节点是否空闲
            p = p << 1;
        } else {                    // 判断右子节点是否空闲
            p = (p << 1) | 1;
        }
    }
    // 计算分配的物理页号 PPN
    usize result = p - sta.firstSingle + sta.startPpn;
    sta.node[p] = 1;    // 标记为已分配
    // 回溯更新父节点
    p >>= 1;            
    while(p >> 0) {
        sta.node[p] = sta.node[p << 1] & sta.node[(p << 1) | 1];    // 若左右子节点都不空闲，则父结点也不空闲
        p >>= 1;
    }
    return result;
}

同样也是从分配处向上回溯，修改节点的值，只不过只需要判断每个节点的子节点是否有空余即可。

5、回收页面：这部分与动态内存分配类似。

// kernel/memory.c

/*
 * 回收物理页
 * 输入物理页号 PPN
 */
void
dealloc(usize ppn)
{
    // 计算页帧在线段树中的索引
    usize p = ppn - sta.startPpn + sta.firstSingle;
    // 如果页表已经空闲则不需要回收
    if(sta.node[p] != 1) {
        printf("The page is free, no need to dealloc!\n");
        return;
    }
    // 标记为空闲
    sta.node[p] = 0;
    // 回溯更新父节点
    p >>= 1;
    while(p > 0) {
        sta.node[p] = sta.node[p << 1] & sta.node[(p << 1) | 1];
        p >>= 1;
    }
}

6、测试线段树的页帧分配

我们定义一个函数，用于同时初始化本节的按页分配和3.2节的动态内存分配：

/*
 * 初始化 页分配 和 动态内存分配
 */
void
initMemory()
{
    // 初始化全局页帧分配器
    initFrameAllocator(
        // 起始PPN 是内核结束虚拟地址-内核起始虚拟地址 再加上 内核起始物理地址 = 内核结束物理地址
        (((usize)(kernel_end) - KERNEL_BEGIN_VADDR + KERNEL_BEGIN_PADDR) >> 12) + 1,
        // 终止页是物理内存的最后一个页
        MEMORY_END_PADDR >> 12
    );
    // 初始化动态内存分配器
    extern void initHeap(); initHeap();
    printf("***** Init Memory *****\n");
}

在main()函数中编写一个测试函数：

// kernel/main.c

void
testAlloc()
{
    printf("alloc %p\n", allocFrame());
    usize f = allocFrame();
    printf("alloc %p\n", f);
    printf("alloc %p\n", allocFrame());
    printf("dealloc %p\n", f);
    deallocFrame(f);
    printf("alloc %p\n", allocFrame());
    printf("alloc %p\n", allocFrame());
}

void main()
{
    extern void initInterrupt();    initInterrupt();    // 设置中断处理程序入口 和 模式
    extern void initTimer();        initTimer();        // 时钟中断初始化
    extern void initMemory();       initMemory();       // 初始化 页分配 和 动态内存分配

    testAlloc();
    
    while(1) {}
}

得到如下输出，可以看到，刚被回收的物理页立刻又被分配出去了。

==== Init Interrupt ====
***** Init Memory *****
alloc 0x0000000080b22000
alloc 0x0000000080b23000
alloc 0x0000000080b24000
dealloc 0x0000000080b23000
alloc 0x0000000080b23000
alloc 0x0000000080b25000

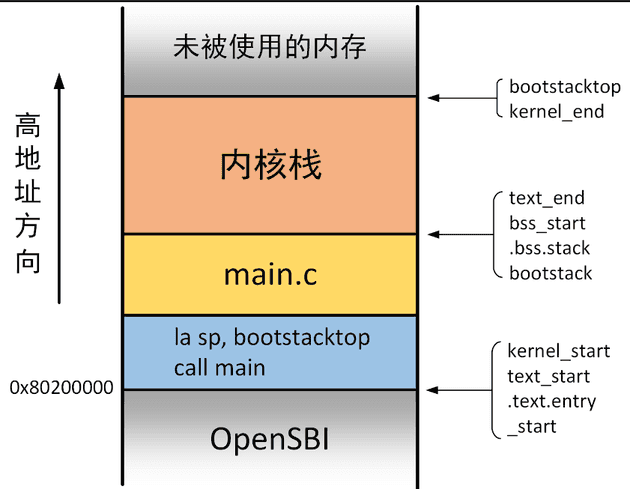
说明：相信到这里，有些同学会觉得混乱、模糊，3.1、3.2节所讲述的动态内存分配和3.3、3.4节所讲述的页帧分配有什么区别？在内核中是怎么存放的？其实内核存放方式可以回到这张图

内核的存放方式定义在kernel.ld文件中，具体是：

0x80000000-0x80200000区间存放OpenSBI监管者二进制接口代码
0x80200000-kernel_end开始分别存放kernel.ld文件中定义的text段、rodata字段、data段、bss段，最后直道内核结束位置kernel_end。我们可以将这个区域统称为操作系统内核。

就比如3.1、3.2节所定义的8M堆区空间，heap.c代码被存放到这个区域的代码段，而HEAP则被存放到这个区域的.bss段，我们称其为内核堆（定义在 .bss 段上 8 MB 大小的字节数组）。故3.2节文末测试发现分配地址为0x0000000080311000

kernel_end-0x88000000这个区间即为未被使用的内存，也称为空闲内存

比如3.3、3.4节所定义的全局页帧分配器FrameAllocator的地址就在这个范围里，故3.4节文末测试发现分配地址为0x0000000080b22000，比HEAP的地址大得多。